Colony growth and using ODEs

←Previous tutorial

In this tutorial, I will illustrate how you can model simple bacterial metabolism, how continuous variables can be shown on the grid, and how ODEs can be attached to grid points. Here are the steps we'll be taking:

Simple colony growth
Populating the grid with custom, unique individuals
Displaying a continuous variable on the grid
Attaching ODEs to grid points

Simple colony growth

From the previous tutorial, you should have a general idea of how to make a simple model. See if you can mimic a simple growing colony, like this:

For my implementation of colony growth, I used the very simple code shown below:

let randomneigh = this.randomMoore8(this,i,j).alive   // Random neighbour        
if(this.grid[i][j].alive == 0)                        // If empty
{
    if(randomneigh == 1 && this.rng.genrand_real1() < 0.5)
        this.grid[i][j].alive = 1                     // 1 ("cell") reproduces
}

The above simulations looks like colony growth, because only the cells at the edge can grow. The limiting resource here is "empty space". However, colony growth should also be limited by nutrient concentrations, and different species may take up resources at different rates. So let's try if we can simulate this. Let's set up a new model called "growth". I have set up a 200x200 grid, and I have disabled the wrapped boundary conditions (like a petri dish, but square :D). The statecolours for 'species' can be manually defined, or simply set to 'default'.

let config =
{
    title: "Colony",                                // The name of your cacatoo-simulation
    description: "",                                // And a description if you wish
    maxtime: 1000000,                               // How many time steps the model continues to run            
    ncol: 200,                                      // Number of columns (width of your grid)
    nrow: 200,		                                // Number of rows (height of your grid)
    seed: 5,
    wrap: [false, false],                           // Wrapped boundary conditions? [COLS, ROWS]   
    scale: 2,				                        // Scale of the grid (nxn pixels per grid point)
    statecolours: {'species': { 1: "#FFFFFF",       // Colours for each state. Background (0) defaults to black.             
                                2: "red",                          
                                3: "#3030ff"}}
    //statecolours: { 'species': 'default' },          
}

sim = new Simulation(config)                        // Initialise the Cacatoo simulation
sim.makeGridmodel("growth")                         // Build a new Gridmodel within the simulation called "model"

Populating the grid

Instead of populating the grid randomly (i.e. what we did in the previous tutorial with "initialGrid"), we will now set it up with some custom individuals. To do this, first define a list (array) of unique individual, and then pass that list on to the function "populateSpot" or "populateGrid":

let species = [{species:1,uptake_rate:0.5,internal_resources:1},
               {species:2,uptake_rate:5.0,internal_resources:1},
               {species:3,uptake_rate:50.0,internal_resources:1}]

sim.populateSpot(sim.growth, species, [0.33,0.33,0.33], 15, config.ncol/2, config.nrow/2)    // Inoculate 1 spot (middle of grid) with species. The third array sets the frequency of each species.
//sim.populateGrid(sim.growth, species, [0.01,0.01,0.01])                                    // Alternatively, inoculate entire grid with species

Above, I have defined three individuals that have different uptake rates. Let's add some "external resource" to the entire grid too, and set up the display for the species.

sim.initialGrid(sim.growth,'external_resources',1000.0,1.0)              // Add 1000.0 external resources to 100% (1.0) of grid points
sim.createDisplay("growth", "species", "Living cells")                   // Create a display in the same way we did in Tutorial 1 (display a discrete variable)

As our three species have a different rate of nutrient uptake, which we can now use these parameters to setup nutrient exchange in the next-state function:

sim.growth.nextState = function (i, j) {
let randomneigh = this.randomMoore8(this, i, j)   // Random neighbour
let this_gp = this.grid[i][j]                     // This cell

if (this_gp.species == 0)                        // If empty spot
{
    if (randomneigh.species > 1 && randomneigh.internal_resources > 50) {   // Random neighbour is alive and it has enough resources
        this_gp.species = randomneigh.species                               // Empty spot becomes the parent type (reproduction)
        this_gp.uptake_rate = randomneigh.uptake_rate                       // Empty spot inherits uptake rate from the parent
        randomneigh.internal_resources = this_gp.internal_resources = randomneigh.internal_resources / 2    // Resources are divided between parent and offpsring
    }
}
else {   
    if (this.rng.genrand_real1() < 0.01) {                                      // Random death
        this_gp.species = 0
        this_gp.uptake_rate=0.0
        this_gp.internal_resources = 0
    }
    else{
        let uptake = this_gp.external_resources * (this_gp.uptake_rate/100)     // Living cells can take up a fraction of available resources
        this_gp.internal_resources += uptake
        this_gp.external_resources -= uptake 
    }
}
}

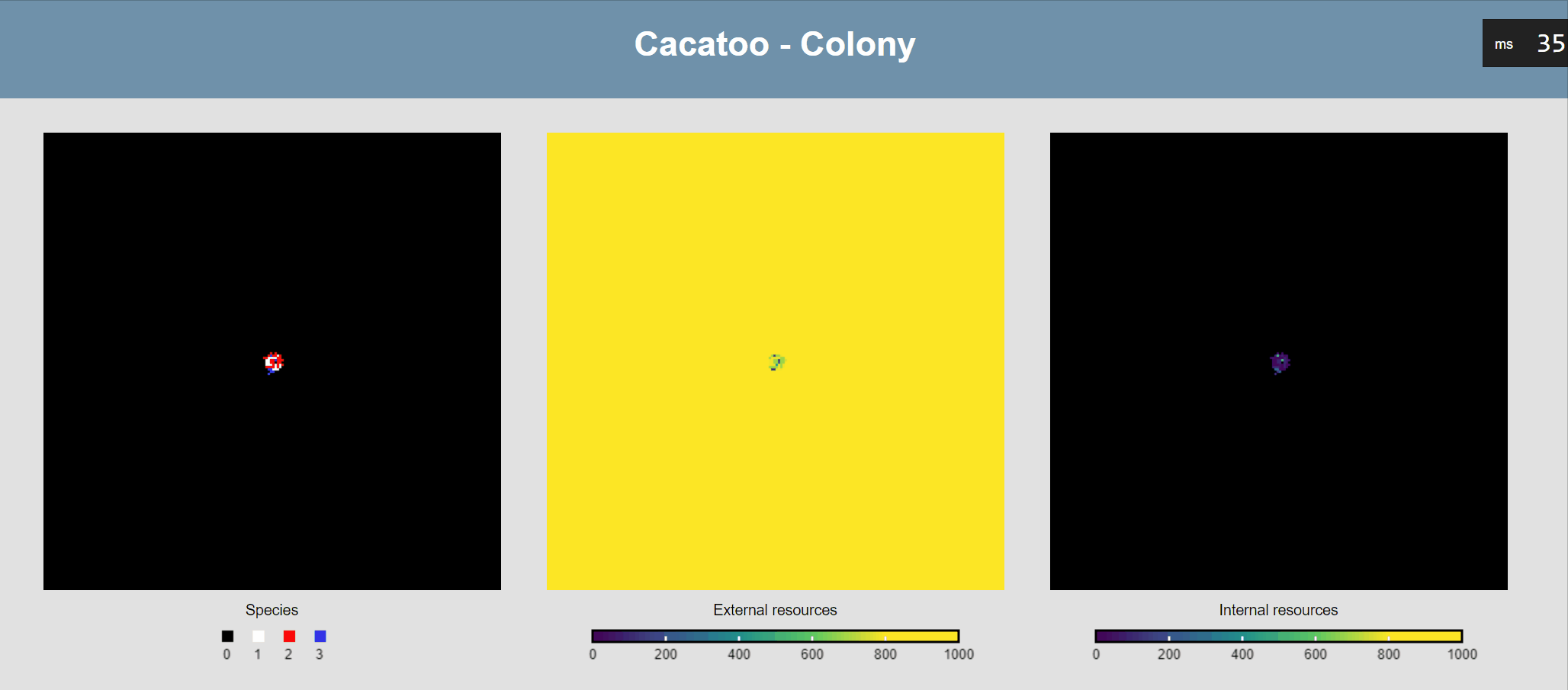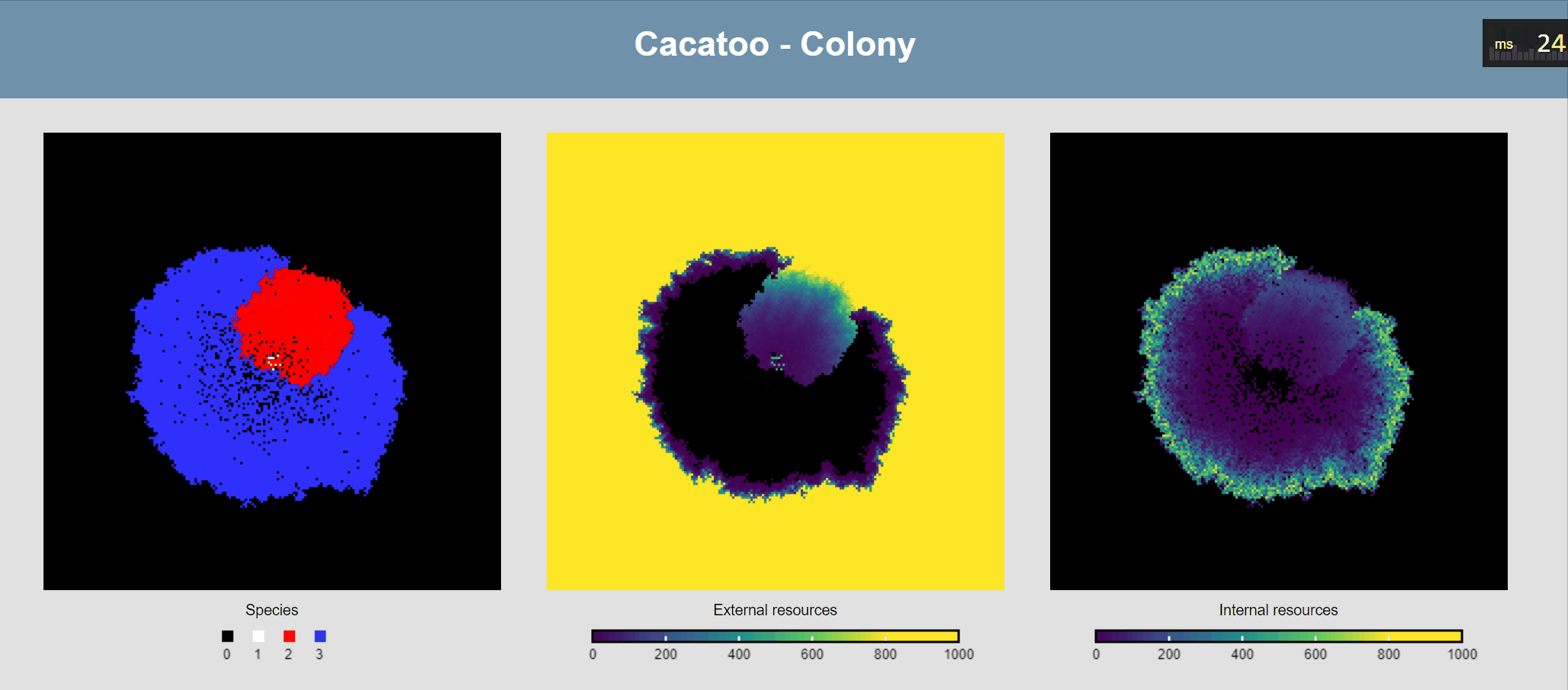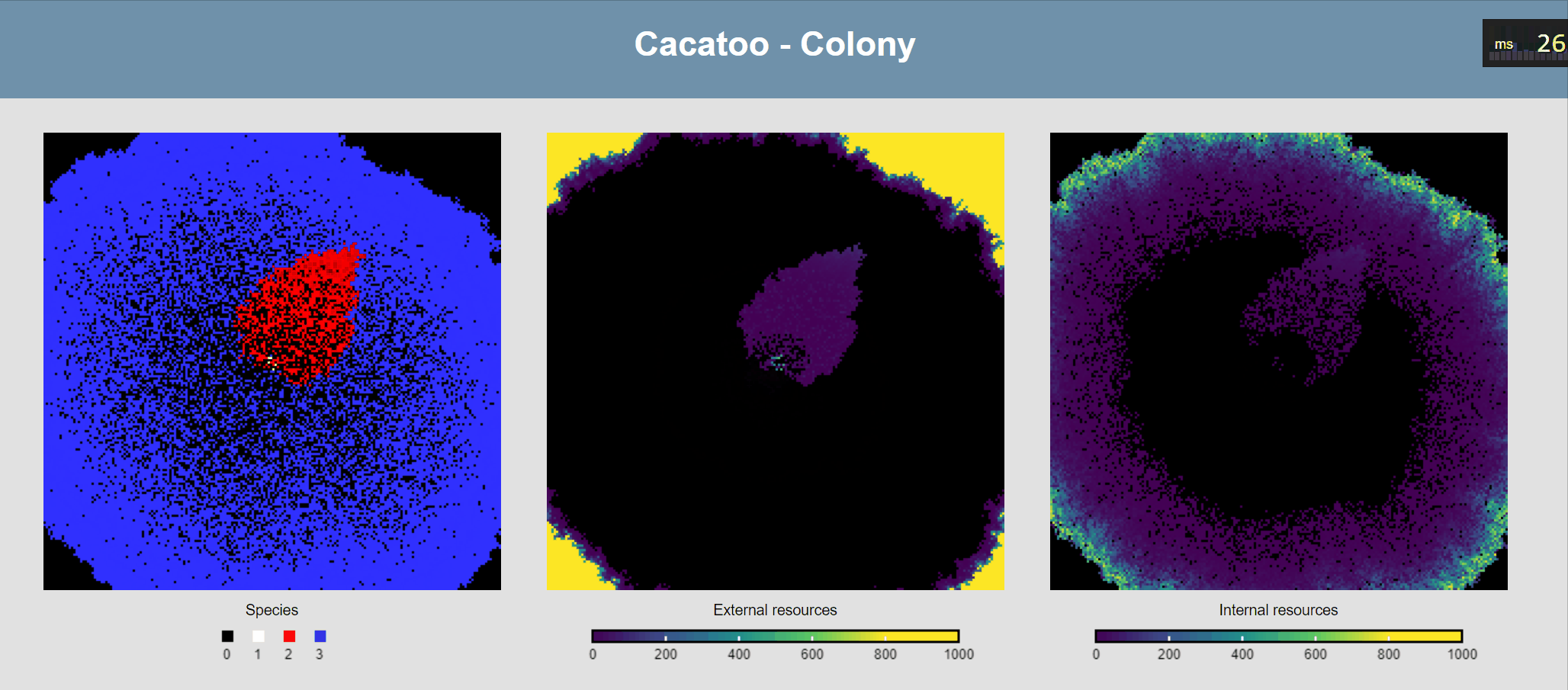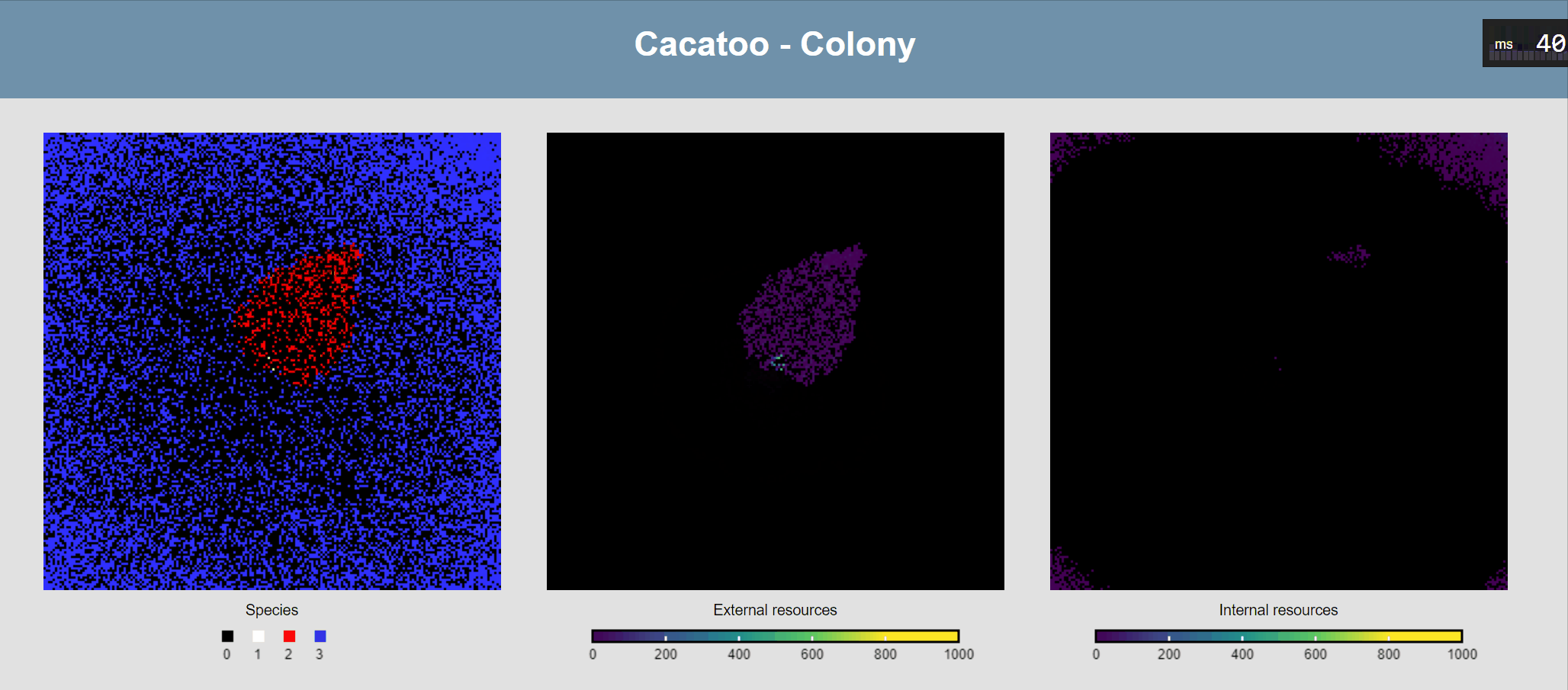
If all goes well, your simulation should now look like this:

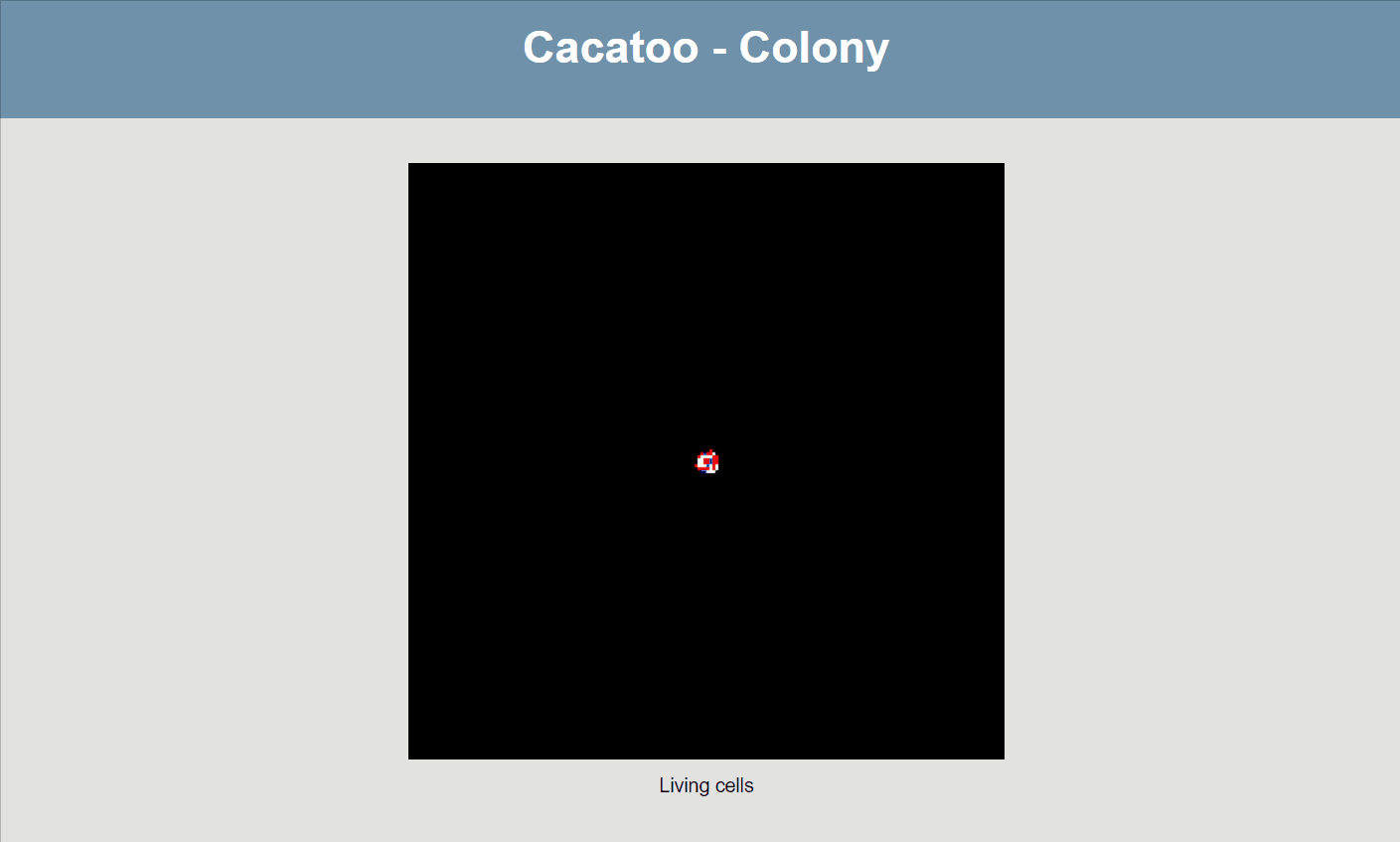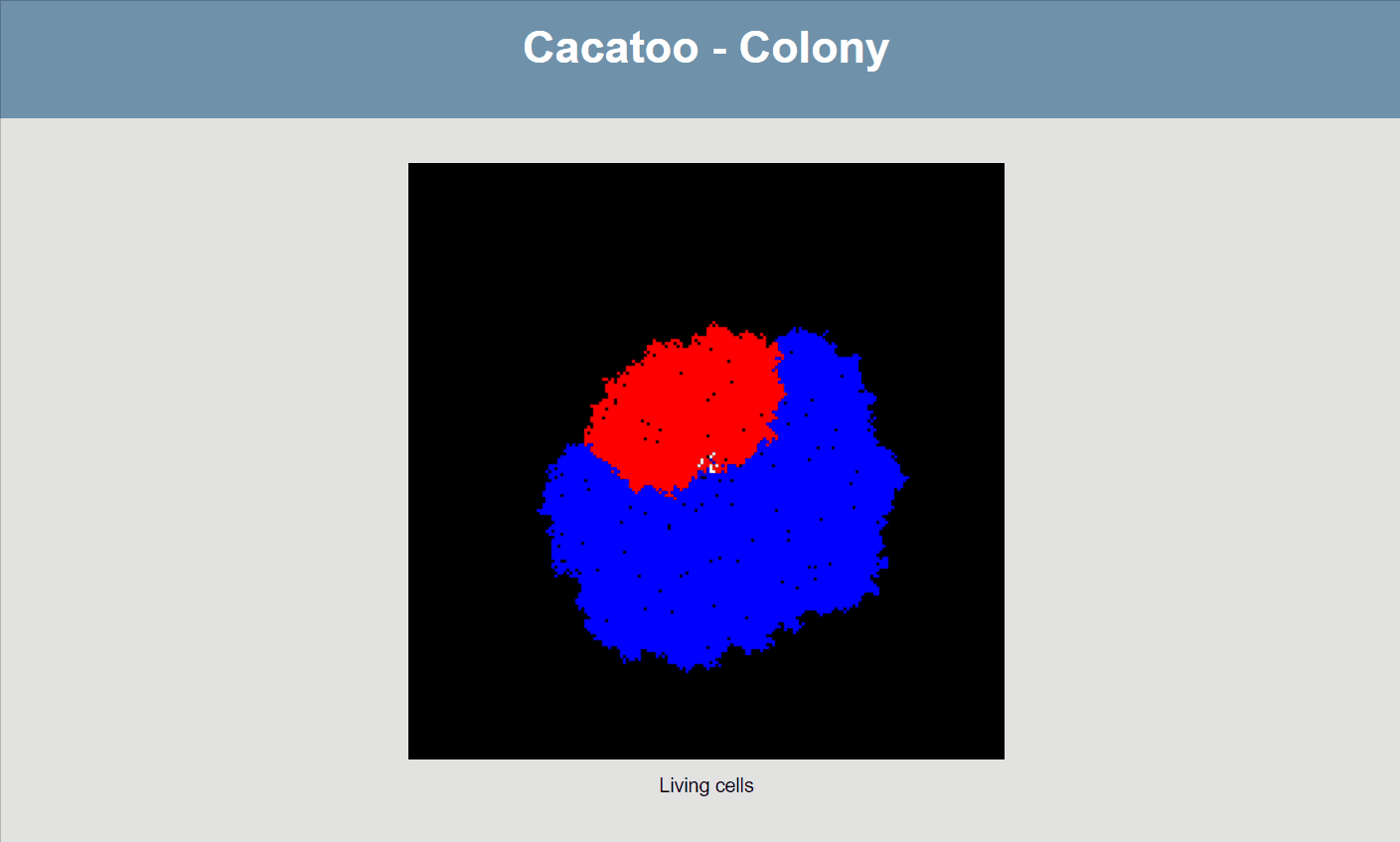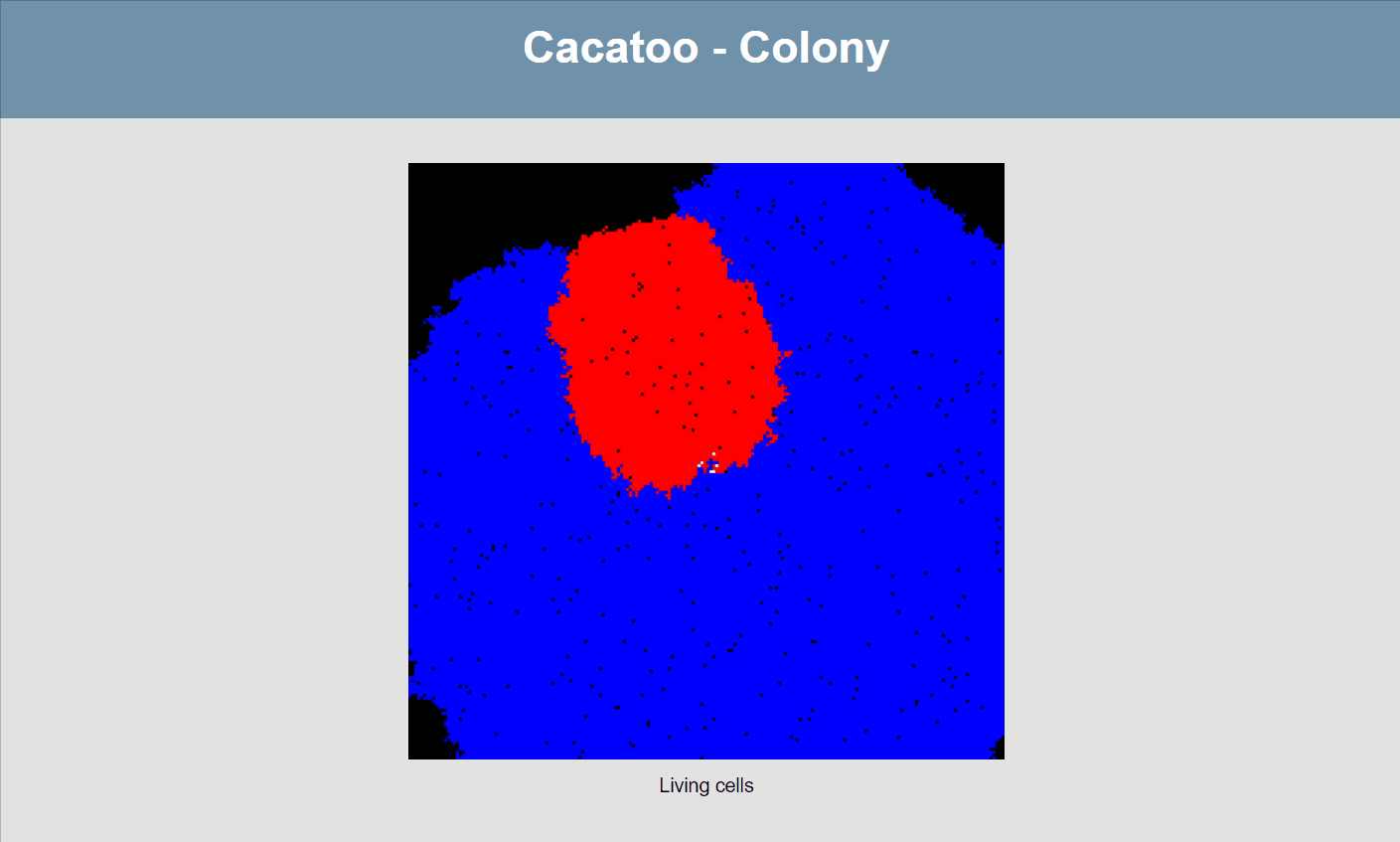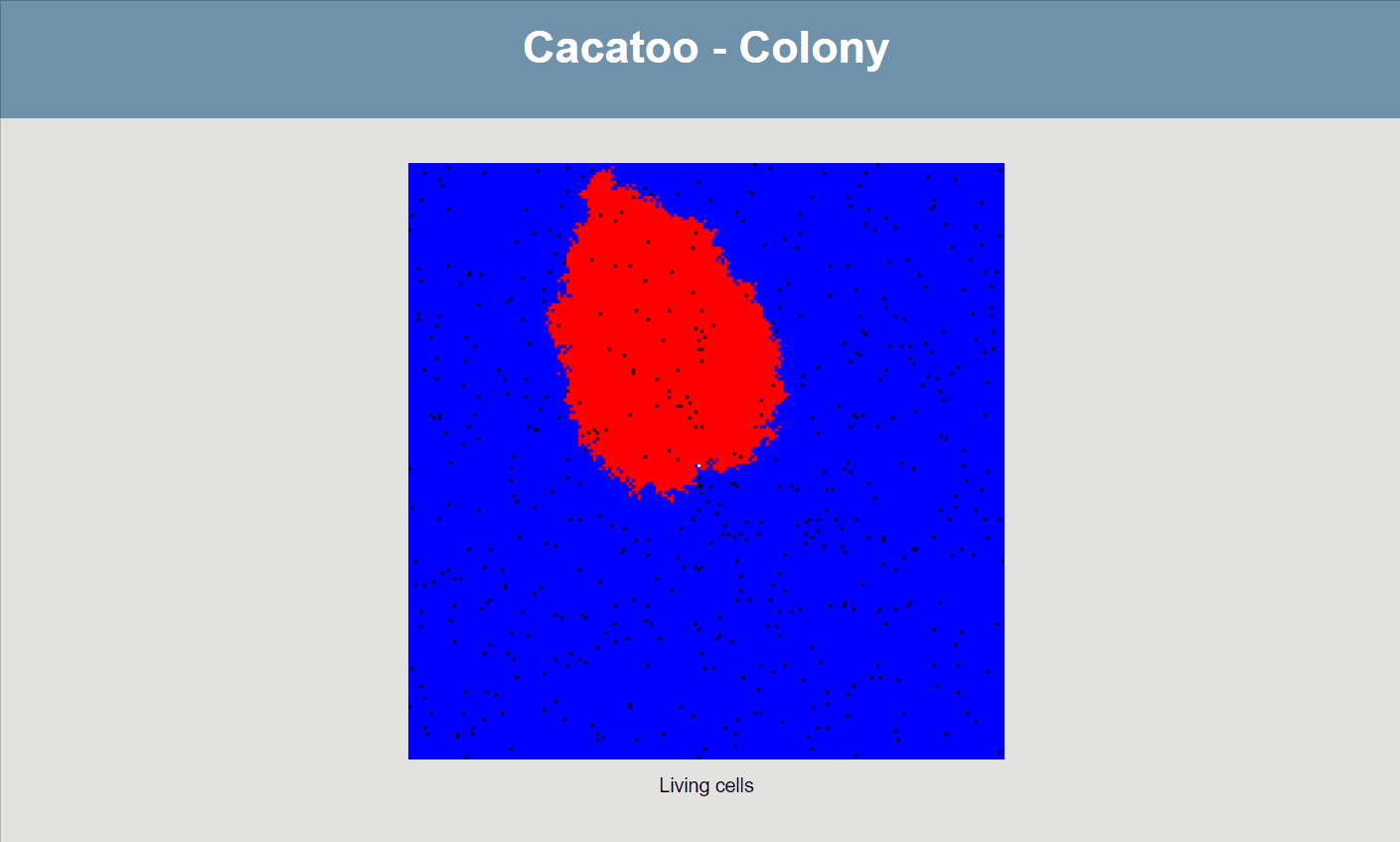
Again, if your simulation isn't working, check out the dev-console to see what the problem is (CTRL/CMD+SHIFT+I in Google Chrome)
The simulation shows that the blue species (high uptake rate) is growing much faster than the red one, and that the white species isn't able to really grow at all! However, it would be better if we could actually see the resource concentrations, both inside and outside of cells.

Displaying a continuous variable

Let's add some displays for these (continuous) variables:

sim.createDisplay_continuous({model:"growth", property:"external_resources", label:"External resources", // Createa a display for a continuous variable (ODE state for external resources)
                minval:0, maxval:1000, fill:"viridis"})                      
sim.createDisplay_continuous({model:"growth", property:"internal_resources", label:"Internal resources", // Createa a display for a continuous variable (ODE state for external resources)
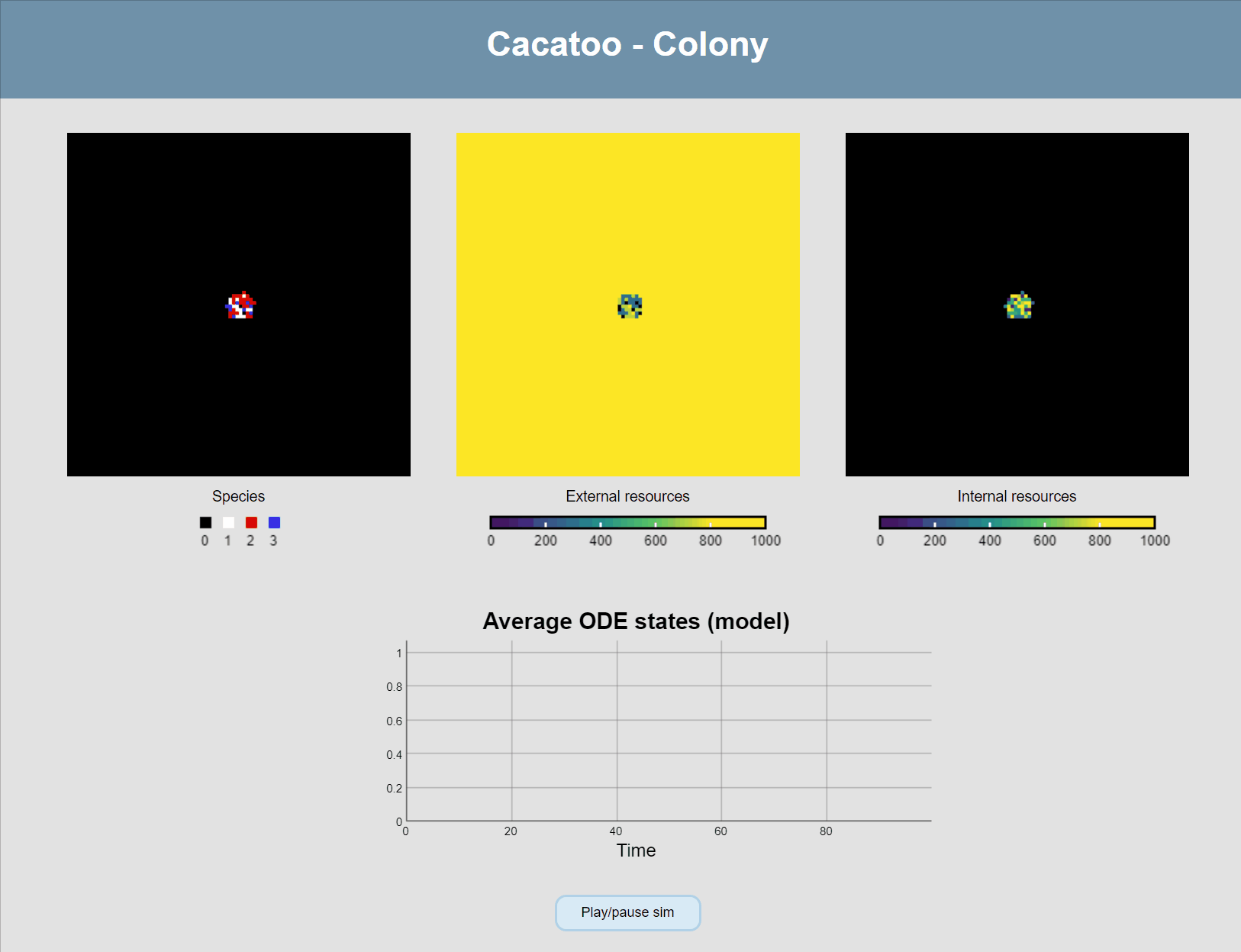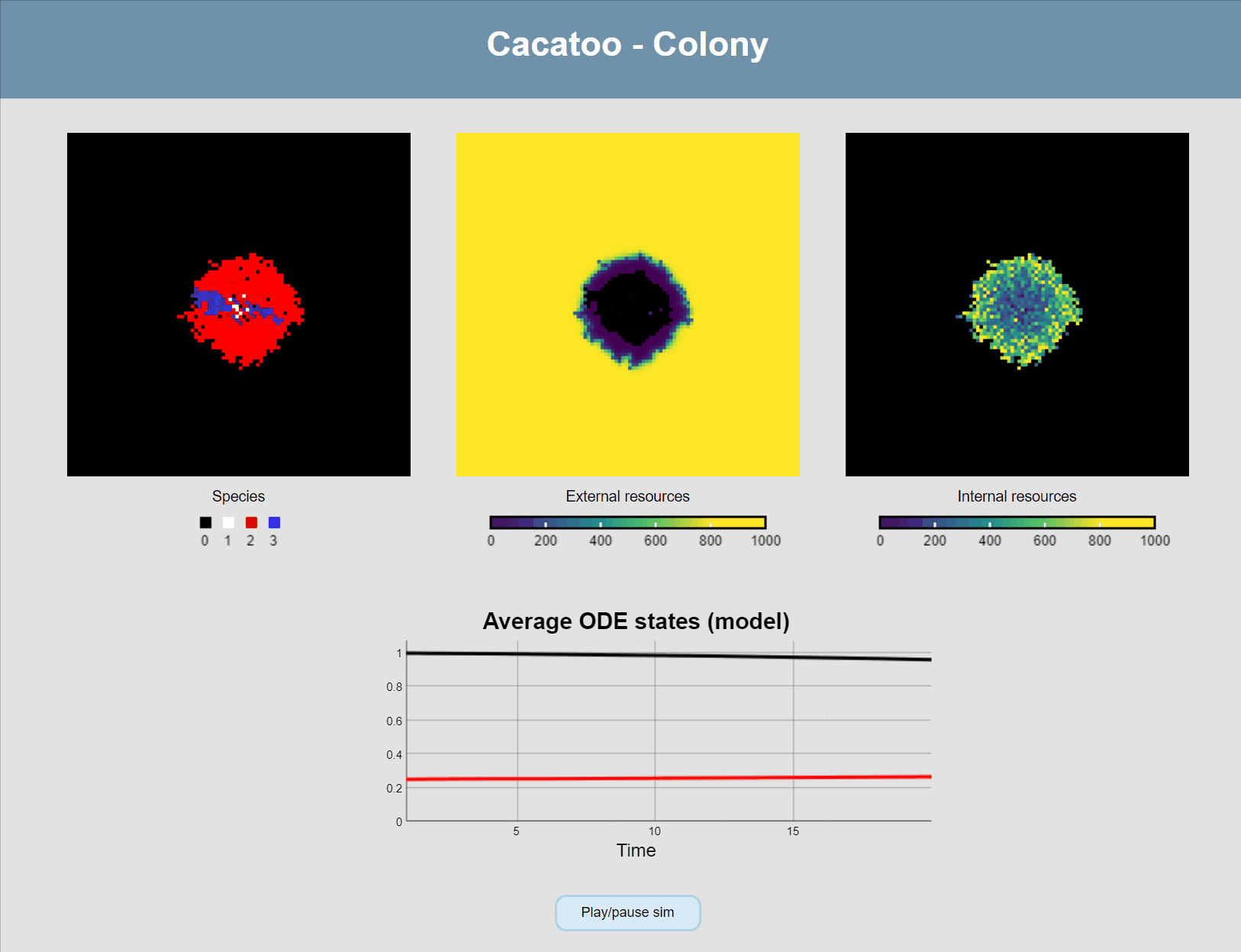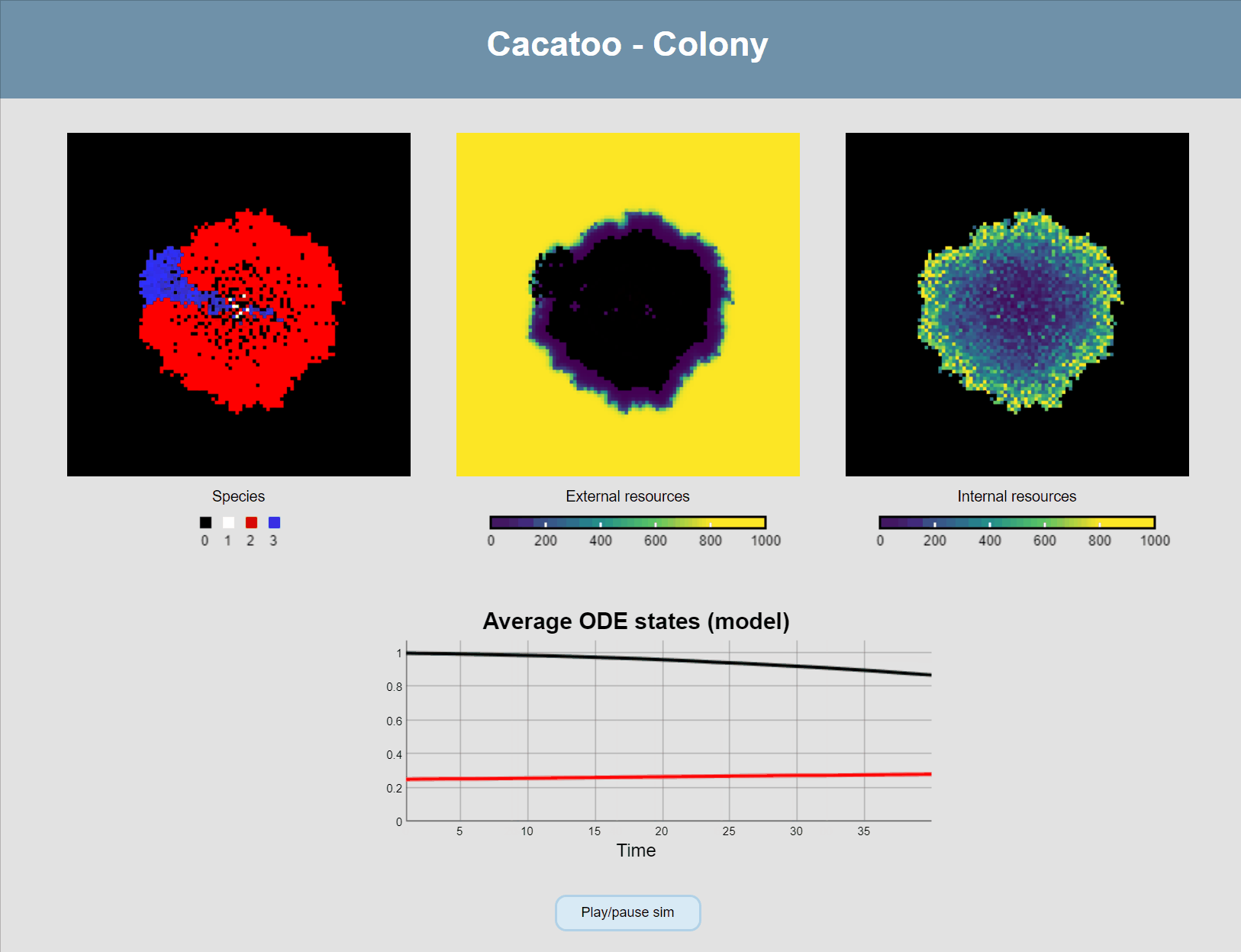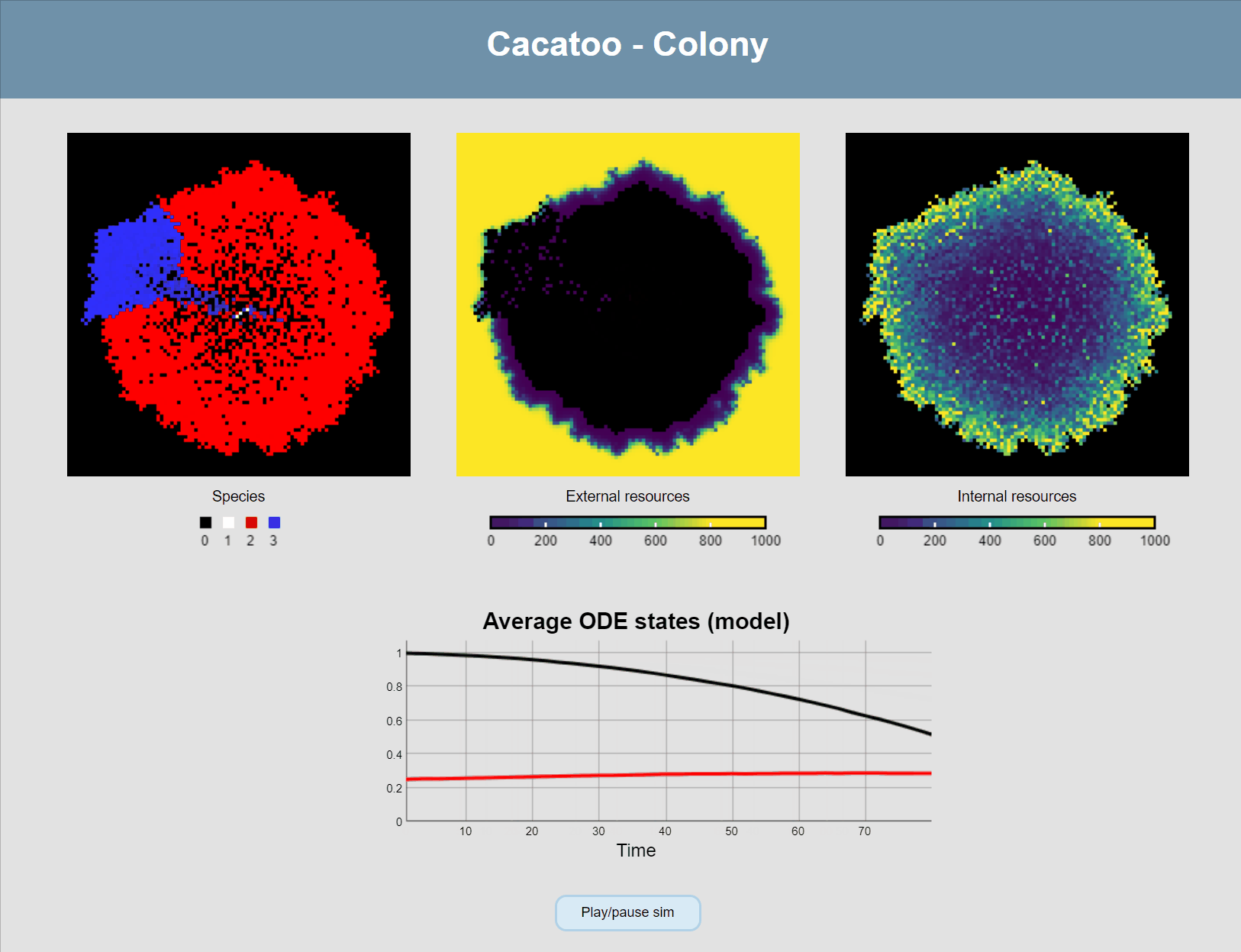
                minval:0, maxval:1000, fill:"viridis"})

As you may notice, the functions above work different from "createDisplay". They only receive one argument, with a configuration-object (similar to how the simulation is initialised). This way it is much easier to setup exactly the display we want, with a custom "fill" function, a minimal cut-off (minval), a maximal cut-off, etc.

If all goes well, you should now see this:

Attach ODEs to grid points

Perhaps you would prefer to use ordinary differential equations (ODEs) to solve the nutrient dynamics. Although numerically solving ODEs is a bit slower than what we did above, it is also much more accurate and allows you to study you favourite ODEs in space! Attaching ODEs to your system is quite easy. Before we define the next-state rule, let's first define a set of ODEs:

// Define ODEs with basic resource dynamics
let resource_dynamics = function (u, k) {
    return function (x, y) {
        let external = y[0] // The first variable (y[0]) is the external resource concentration, which is taken up with rate u
        let internal = y[1] // The second variable (y[1]) is the internal resource concentration, which is used by the cells to divide
        return [   -u * external,                 
                    u * external - k * internal ]
    }
}
// Configuration object with initial states, parameters, and diffusion rates
let ode_config = {
    ode_name: "resources",
    init_states: [1, 0],              // Initial values of external and internal resources
    parameters: [0.0, 0.0],           // u and k are set to 0.0 by default, as we will make it dependent on cell presence!
    diffusion_rates: [0.2, 0.0]       // resources diffuse through exteral environment, but internal resources stay inside cells
}      

// Attaches an ODE to all gridpoints with the given configuration object
sim.model.attachODE(resource_dynamics, ode_config);

At this point, your model won't really do anything different. This is because, although the grid points have ODEs within them, they are not yet being solved. Below I modify the next-state function such that i) only grid points with a cell inside have their "uptake" parameter set, ii) the internal resource variable is divided between parent and offspring update-function reproduction, and iii) all grid-points get solved. The rest should function approximately the same as our model above.

sim.model.nextState = function (i, j) 
{
    let randomneigh = this.randomMoore8(this, i, j)   // Random neighbour
    let this_gp = this.grid[i][j]                     // This cell

    if (this_gp.species == 0)                        // If empty
    {
        if (randomneigh.species > 1 && randomneigh.resources.state[1] > 0.5) {
            this_gp.species = randomneigh.species
            this_gp.uptake_rate = randomneigh.uptake_rate
            randomneigh.resources.state[1] = this.grid[i][j].resources.state[1] = randomneigh.resources.state[1] / 2
        }
    }
    else {
        this.grid[i][j].resources.pars = [this_gp.uptake_rate, 0.5]  // Living cells take up and have upkeep
        if (this.rng.genrand_real1() < 0.01) {
            this_gp.species = 0
            this_gp.uptake_rate=0.0
            this_gp.resources.state[1] = 0
            this_gp.resources.pars = [0.0, 0.0]
        }
    }

    this_gp.resources.solveTimestep(0.1) // Solve a single time step with delta_t=0.1

    this_gp.external_resources = this_gp.resources.state[0]
    if(this_gp.species > 0) this_gp.internal_resources = this.grid[i][j].resources.state[1]
    else this.grid[i][j].rersources = 0.0 
}

And one final thing we want to do is modify the main update-loop to add diffusion of the ODE states between grid points (i.e. the external resources), and add a plot so we can see the concentrations changing:


    sim.model.update = function () {
        this.asynchronous()         // Applied as many times as it can in 1/60th of a second
        this.diffuseODEstates()       // Diffusion of external metabolites
        this.plotODEstates("resources", [0, 1], [[0, 0, 0], [255, 0, 0]])
    }